GAMES202

• 1 Introdution
• 2 Recap of CG Basics
  • Graphics Pipeline
  • OpenGL
  • The Rendering Equation
• 3 Real-Time Shadows
  • Shadow Map
  • Percentage Closer Filtering
  • Percentage Closer Soft Shadow
  • Variance Soft Shadow Map
  • Cascaded Shadow Map
• 4 Real-Time Environment Map
  • Recap: Image-Based Lighting
  • Split Sum Approximation
  • Precomputed Radiance Transfer
• 5 Real-Time Global Illumination
  • Reflective Shadow Maps
  • Light Propagation Volumes
  • Voxel Global Illumination
  • Screen Space Ambient Occlusion
  • Horizon Based Ambient Occlusion+
  • Screen Space Directional Occlusin
  • Screen Space Reflection

1 Introdution

Real-Time High Quality Rendering:

• 实时性：30 frame per second（对于VR/AR，要求可能到90FPS）；
• 高质量：尽可能保证结果真实，即对错误容忍度低；

4 Different Parts of Real-Time Rendering：

• 阴影
• 全局光照
• 基于物理的着色
• 实时光线追踪

Motivation of Real-Time Rendering：

目前，计算机图形学中的技术已经支持生成一些极逼真的图像，但这些方法大多耗时过长，比如光线追踪等。因此，出现了一系列针对实时渲染的研究，它们的目的就是牺牲一小部分准确性，来获取较高质量的快速渲染。

Evolution of Real-Time Rendering：

• 20年前：图形硬件（SGI/GPU）出现，大部分重点放在几何图形和纹理映射上，同时出现了一些调增强真实感的技术：阴影映射、累积缓冲区等。
• 10年到20年前：着色器出现（可编程图形硬件），更多复杂的图形渲染技术出现，比如：环境光、软阴影等
• 目前：VR/AR

Technological and Algorithmic Milestones：

• 20年前：可编程图形硬件（着色器）
• 15年前：基于预计算的渲染方法
• 8-10年前：交互式光线追踪

2 Recap of CG Basics

Graphics Pipeline

OpenGL

A Set of API：

OpenGL是一组可编程渲染管线API的封装。它的特点包括：

• 跨平台；
• 很多替代技术，比如：DirectX和Vulkan；
• C风格的。

Analogy: Oil Painting：

使用OpenGL渲染的流程其实和画油画类似，包括以下几个步骤：

• 创作油画的第一步是摆放物品/模型。类似的，渲染的第一步则是准备好待渲染模型的顶点数据，包括：顶点、法线以及纹理坐标等，并在稍后使用顶点缓存对象（Vertex Buffer Object，VBO）将其传入给GPU。
• 创作油画的第二步是摆好画架。类似的，渲染的第二步则是设置好相机位置，进行视图转换（View Transformation）。同时，还要创建顶点

The Rendering Equation

BRDF：

双向反射分布函数（Bidirectional Reflectance Distribution Function，BRDF）是真实感图形学中最核心的概念之一，它描述的是物体表面将光能从任何一个入射方向反射到任何一个视点方向的反射特性，即入射光线经过某个表面反射后如何在各个出射方向上分布。

Cook-Torrance BRDF：

Cook-Torrance BRDF是一种目前最流行一种BRDF反射模型，它包含漫反射和镜面反射两个部分：$f_r=k_df_{lambert}+k_sf_{cook-torrance}$。其中，$f_{lambert}=\frac\rho\pi$，而$f_{cook-torrance}=\frac{DFG}{4(\vec{w_o}\vec{n})(\vec{w_i}\vec{n})}$。

3 Real-Time Shadows

Shadow Map

阴影贴图是目前最主流的阴影生成算法。这主要得益于它算法直观，并且能够充分利用现代硬件的光栅化能力。具体来说，它的核心思路基于一个假设，即对于指定光源来说，场景中某个点是否被其照亮，取决于从光源的视角看去，这个点是否可见。

Two-Pass Algorithmn：

因此，该算法被分成了两步：

• 从光源的视角出发，绘制整个场景（平行光用正交投影，点光用透视投影），生成深度图，即所谓的阴影贴图；
• 从摄像机视角出发，重新绘制场景，并根据光源投影矩阵的逆矩阵，将世界坐标空间变换回光源的投影空间，找出对应投影空间UV坐标以及投影空间内的深度d。

此时，就可以使用光源投影空间的UV坐标和阴影贴图，得到深度z。比较深度z和深度d，若d>z，则当前位置被遮挡，处于阴影内；反之，则未被遮挡。

可见，阴影贴图是一个完全在图像空间中的算法。它的优点是一旦贴图已经生成，则其就可以作为场景中的几何表示(场景中所有位置在光源处的深度)，而不用再去获取场景中的其他信息。而缺点则是算法会产生自遮挡和走样现象。

Simple Implementation with GLSL：

了解了阴影贴图的流程之后，我们可以简单实现它。比如：Phase 1中预生成阴影纹理的片元着色器如下。

#ifdef GL_ES
precision mediump float;
#endif

uniform vec3 uLightPos;
uniform vec3 uCameraPos;

varying highp vec3 vNormal;
varying highp vec2 vTextureCoord;

vec4 pack (float depth) {
    // 使用rgba 4字节共32位来存储z值,1个字节精度为1/256
    const vec4 bitShift = vec4(1.0, 256.0, 256.0 * 256.0, 256.0 * 256.0 * 256.0);
    const vec4 bitMask = vec4(1.0/256.0, 1.0/256.0, 1.0/256.0, 0.0);
    // gl_FragCoord:片元的坐标,fract():返回数值的小数部分
    vec4 rgbaDepth = fract(depth * bitShift); //计算每个点的z值
    // Cut off the value which do not fit in 8 bits
    rgbaDepth -= rgbaDepth.gbaa * bitMask; 
    return rgbaDepth;
}

void main(){
  gl_FragColor = pack(gl_FragCoord.z);
}

Phase 2中显示的片元着色器如下：

float unpack(vec4 rgbaDepth) {
  const vec4 bitShift = vec4(1.0, 1.0/256.0, 1.0/(256.0*256.0), 1.0/(256.0*256.0*256.0));
  return dot(rgbaDepth, bitShift);
}

float useShadowMap(sampler2D shadowMap, vec4 shadowCoord){
  float d = unpack(texture2D(shadowMap, shadowCoord.xy));
  if (shadowCoord.z > d + EPS) {
    return 0.0;
  } else {
    return 1.0;
  }
}

void main(void) {

  //vPositionFromLight为光源空间下投影的裁剪坐标，除以w结果为NDC坐标
  vec3 shadowCoord = vPositionFromLight.xyz / vPositionFromLight.w;
  //把[-1,1]的NDC坐标转换为[0,1]的坐标
  shadowCoord = (shadowCoord + 1.0) / 2.0;

  // 计算是否为阴影（因为是硬阴影，所有返回值仅为0或1）
  float visibility = useShadowMap(uShadowMap, vec4(shadowCoord, 1.0));
  // 计算颜色
  vec3 phongColor = blinnPhong();

  gl_FragColor = vec4(phongColor * visibility, 1.0);
}

Issues in Shadow Map：

阴影失真（Shadow Acne）是阴影贴图中最容易出现的问题。它表现为在阴影区域出现间隔的条纹，如下图所示。

出现这种现象的原因在于ShadowMap中的每个texel只能记录一个深度值，但一个像素内的不同位置可能会有不同的深度值（即，试图用离散的纹理去记录连续的信息）。因此，当实际场景的深度值大于ShadowMap上记录的深度值时，就会出现Shadow Acne现象。

一个简单通用的解决方案是在比较前给d加上一个固定偏移。但是若偏移选取过大，又会产生所谓的阴影悬空（Peter-Panning）问题，如下图所示。

改进的方法则是添加自适应偏移的方案，即基于斜率去计算当前深度要加的偏移（Slope Scale Depth Bias）。

另外，阴影走样（Shadow Aliasing）也是阴影贴图中容易出现的问题。比如

其原因则是阴影贴图是一个大小不足，造成多个片段对应一个纹理像素。工业界的解决办法是，不同位置采用不同分辨率的shadow map，或者是动态分辨率之类的技术，也可以直接用PCF生成软阴影。

除此之外，阴影贴图还存在纹理利用不足的问题。因为相机和光源视角不同，所以从光源视角光栅化后的每个像素投影到屏幕空间后，对应的区域大小也不相同，进而引发靠近相机位置的阴影贴图精度不够，而远离相机位置的阴影贴图精度又过高的问题。改善这种利用率不足的方法包括：级联阴影贴图和Sample Distribution Shadow Map。

Percentage Closer Filtering

百分比渐进滤波（Percentage-Closer Filtering，PCF）是一种滤波工具。它可以改善阴影的平滑度和真实感，减少硬边缘和锯齿效果。

PCF并非在直接在最后生成的结果上做模糊，或是对Phase1计算得到阴影贴图进行模糊，而是在做阴影判断时进行滤波操作从而生成更合理的visibility。因为已经出现走样即高频重叠后，再去进行模糊是无法消除重叠的；而对阴影贴图进行模糊并不能改善visibility返回值非0即1的情况。

具体来说，其原理就是计算visibility时，在原阴影贴图坐标一定范围中，选择若干随机点；将这些点的深度值，和原点的深度值作比较，最后将其加和取平均即可。其在GLSL中的实现如下：

float PCF(sampler2D shadowMap, vec4 coords, float filterSize) {
  float visibility = 0.0;

  poissonDiskSamples(coords.xy);
  for (int i = 0; i < NUM_SAMPLES; i++) {
    // 偏移量 = 0到1随机变量 * 归一化后的采样半径
    vec4 offset = vec4(poissonDisk[i], 0, 0) * filterSize;
    // 采样点位置 = 实际位置 + 偏移量
    float d = useShadowMap(shadowMap, coords + offset);
    if (d + EPS > coords.z) {
      visibility = visibility + 1.0;
    }
  }
  // 取平均
  return visibility / float(NUM_SAMPLES);
}

Percentage Closer Soft Shadow

如下图所示，在真实世界中，笔尖的阴影十分锐利，而笔杆的阴影会软一些。

由此，我们可以得出结论：

• 承载阴影的物体表面点与阴影产生物的距离越小，阴影越硬。
• 阴影的软硬与光源距离无关，与遮挡物距离有关

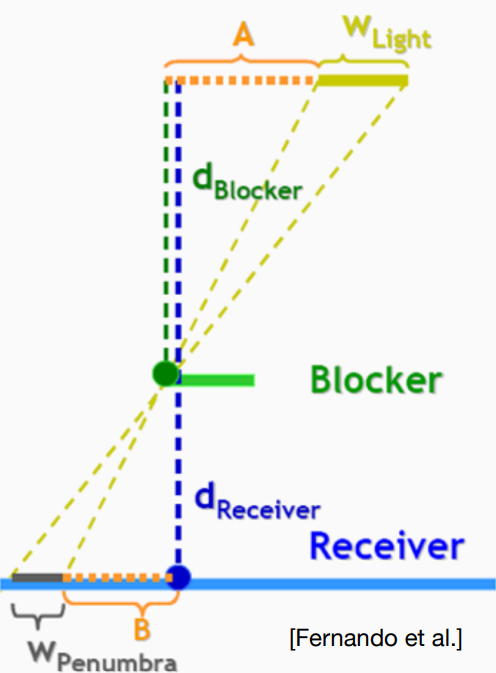
进一步，我们可以根据相似三角形定理从上述示意图中推导出一个公式，这也是PCSS的核心。

$$ \frac{W_{Penumbra}}{W_{Light}}=\frac{d_{Receiver}-d_{Blocker}}{d_{Blocker}} $$

其中，$W_{Penumbra}$表示软阴影大小；$W_{Light}$表示光源大小；$d_{Receiver}$表示光源到片元的距离；$d_{Blocker}$表示光源到遮挡物的距离。

百分比渐进软阴影（Percentage Closer Soft Shadow, PCSS）技术是对PCF的进一步改进，它能实现更逼真的阴影效果，即阴影的软硬会随承载阴影的物体表面与阴影产生物的距离变化。换句话说，它能根据上述原理针对不同片元生成自适应软阴影大小，也即上述PCF实现中使用的采样范围。其GLSL实现如下：

float findBlocker(sampler2D shadowMap, vec2 uv, float zReceiver, float searchRange) {
  float depthSum = 0.0;
  int blockerNum = 0;

  poissonDiskSamples(uv);
  for (int i = 0; i < NUM_SAMPLES; i++) {
    float d = unpack(texture2D(shadowMap, uv + poissonDisk[i] * searchRange));
    if (d + EPS < zReceiver) {
      depthSum = depthSum + d;
      blockerNum = blockerNum + 1;
    }
  }

  if (blockerNum == 0) {
    return 0.0;
  }

  return depthSum / float(blockerNum);
}

float PCSS(sampler2D shadowMap, vec4 coords, float searchRange){

  // STEP 1: avgblocker depth
  float avgDepth = findBlocker(shadowMap, coords.xy, coords.z, searchRange);

  // STEP 2: penumbra size
  if (avgDepth == 0.0) {
    return 1.0;
  }
  float penumbraSize = (coords.z - avgDepth) / avgDepth * LIGHT_SIZE;

  // STEP 3: filtering
  float visibility = PCF(shadowMap, coords, penumbraSize);

  return visibility;
}

Variance Soft Shadow Map

PCSS、PCF的算法都需要多重采样，尤其PCSS需要两个多重采样（第一步的Blocker Search和第三步的PCF），这使得算法速度较慢。为了避免多重采样的计算，方差阴影贴图（Variance Shadow Map, VSM）和方差软阴影贴图（Variance Soft Shadow Map, VSSM）被提出了。

其中，VSM假定阴影贴图中一定范围内的深度符合正态分布。那么只要计算出该范围的深度均值E和方差Var，就能根据正太分布的概率密度函数快速得出该范围中有多少比例大于某个指定深度，从而计算出该位置片元的visibility。至于VSSM则是PCSS对应的版本，即先用概率密度函数估计平均遮挡物深度，再通过平均遮挡物深度计算软阴影半径，进而得出片元visibility。

此外，在VSM和VSSM中，均值和方差都不通过采样去得到，而是依靠硬件实现。具体来说，均值E是通过纹理mipmap来实现的。而方差根据公式$Var(X)=E(X^2)-E^2(X)$，只需要额外存储一张深度平方贴图即可通过类似的方法快速得出。

尽管VSSM用于不错的计算速度，但大胆的假设使得其仅仅在真实深度分布为某个单峰曲线才比较符号物理，这也是它的问题。

Cascaded Shadow Map

由于相机和光源视角不同，从光源视角光栅化后的每个像素投影到屏幕空间后，对应的区域大小也不相同，所以往往会出现距离相机较近位置的Shadow Map精度不够，而距离相机较远位置的Shadow Map精度又过高的问题，于是就会出现阴影边缘的明显锯齿。

缓解这个问题的方法是把视锥沿着Z轴切分成多段，每段单独计算出一个光源坐标空间内的紧凑AABB，然后基于这个AABB生成多张Shadow Map，也就是所谓的级联式阴影（Cascaded Shadow Map）。在进行深度查询时，首先根据当前像素在相机空间中的Z值确定其位于哪个分段中，然后找到对应分段的Shadow Map和投影矩阵。在实际操作中，通常会选择3~4级分段，划分位置通常是指数划分和均匀划分的结果进行插值后得到。鉴于划分是基于视锥的，所以较远处的Shadow Map可以预先计算好，或者每隔几帧才更新一次，以此提高渲染效率。

Issues in CSM:

级联阴影之间有时会因为前后两层的分辨率不同而产生阴影间隙，如上图所示。解决办法则是使用前后两张阴影贴图进行线性插值。

除此之外，由于使用紧凑AABB划分视锥，那么视锥的一些微小变换就可能造成阴影贴图的有效分辨率大大减小。一种合理的解决方案则是使用球体包围盒代替紧凑AABB。

关于级联阴影更多的问题，可以参考这篇文章。

4 Real-Time Environment Map

Recap: Image-Based Lighting

基于图像的光照(Image Based Lighting, IBL)是使用图片表示场景中所有光照的技术。它通常是一个包含场景周围环境的全景图像或立方体贴图，其中每个像素都被视作一个光源。

Split Sum Approximation

learnopengl中镜面反射IBL

Prefiltered Environment Lighting:

IBL下的渲染仍然是解决渲染方程，在不考虑visiblity项前提下，使用积分差分法近似出射光辐射度，可得渲染方程如下：

$$ \begin{align} L_o(p, w_o) &= \int_{\Omega}{L_i(p, w_i)f_r(p, w_i, w_o)cos\theta}dw_i\ &\approx \frac{\int_{\Omega_{f_r}}L_i(p, w_i)dw_i}{\int_{\Omega_{f_r}}dw_i}\int_{\Omega}{f_r(p, w_i, w_o)cos\theta}dw_i \end{align} $$

其中，拆分得到的第一项其实就是对入射光辐射度的一个模糊处理，即对其进行平滑滤波并除以一个定值。不过，需要注意的是第一项的积分域为$\Omega_{f_r}$，也即受$f_r$影响，因此需要针对不同的$f_r$（即粗糙度）进行平滑滤波，最终得到下图所示效果。

Look-Up Texture:

至于第二项，则可以通过下图中的公式进行计算。

Precomputed Radiance Transfer

预计算辐射度传输（Precomputed Radiance Transfer，PRT） 是一类基于预计算渲染方法。它将渲染方程中入射光项$L_i$和非入射光项$V\cdot{f_r}\cdot{cos\theta}$分别用一系列基函数近似，并将方程中将时域上的积分转换为频域上的乘积，从而达到快速计算的目的。

Spherical Harmonics：

一般来说，PRT选择球谐函数（Spherical Harmonics, SH）作为其基函数。而球谐函数是一系列定义在二维球面中的函数。

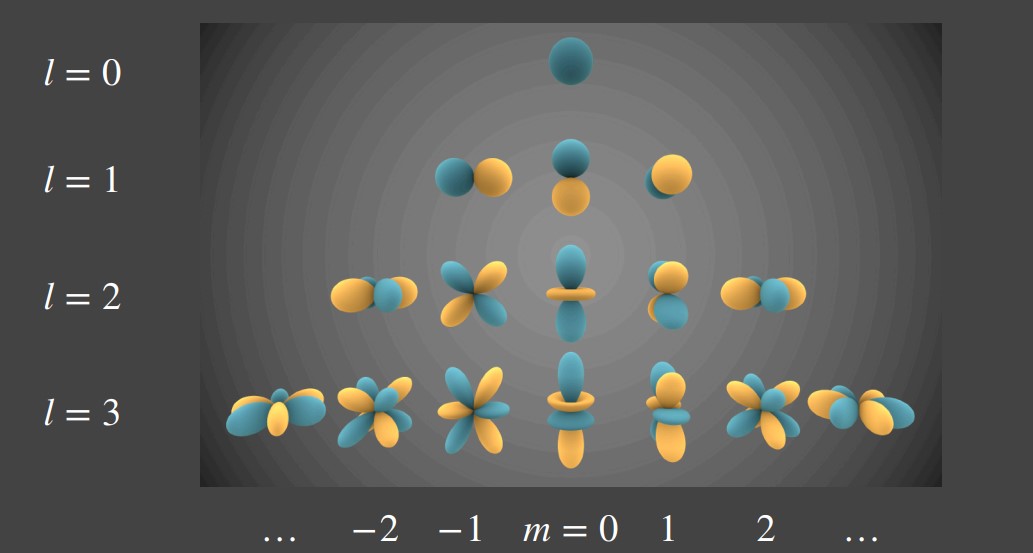
Light/Light Transport Coefficents：

前面提到渲染方程中入射光项和非入射光项可分别用球谐函数近似，即：$L_i=\sum{l_iB_i(i)}$和$V\cdot{f_r}\cdot{cos\theta}=\sum{t_iB_i(i)}$。

而其中系数其实就是待表达项在对应球谐函数上的投影，即：$l_i=\int_\Omega{L(i)B_i(i)di}$。

而整个输出光辐射度则可根据球谐函数正交的特点化简为$L_o(i)\approx\sum{l_it_i}$。

5 Real-Time Global Illumination

全局光照（Global Illumination, GI）就是直接光照+间接光照。在实时渲染中，GI技术通常只考虑一次弹射的间接光，它们可按处理阶段分为：

• 3D空间GI技术：RSM、LPM和VXGI等；
• 屏幕空间GI技术：SSAO、SSAO+、HSAO和SSR等。

其中，屏幕空间方法都可以视作一种图像后处理，因为它仅仅利用了图像中的信息，比如：深度信息和阴影贴图等。

Reflective Shadow Maps

反射阴影贴图（Reflective Shadow Maps, RSM）是一种3D空间的全局光照技术。它将任何能够接收到直接光照的片元视作次级光源，同时假设次级光源总是diffuse的，即次级光源的任意出射辐射度相同。

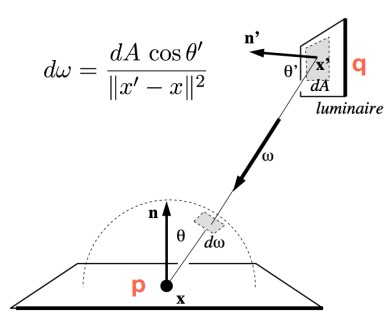
由此，下图中某位置p接收到的q处发射的间接光，可表示为：

$$ \begin{align} L_o(p,w_o)=&\int_{\Omega_{patch}}{L_i(p,w_i)V(p,w_i,w_o)f_r(p,w_i,w_o)cos\theta_{p}dw_i}\ =&\int_{A_{patch}}{L_i(p,q\rightarrow p)V(p,q\rightarrow p,w_o)f_r(p,q\rightarrow p,w_o)\frac{cos\theta_{p}cos\theta_{q}}{||p-q||^2}dA}\ \end{align} $$

其中，根据次级光源总是diffuse的假设，q处发射的间接光又可以表示为：

$$ \begin{align} L_o(q,w_o)=&\int_\Omega{L_{light}f_r(p,w_i,w_o)cos\theta_{q}dw_i}\ =&\frac{albedo}{\pi}\int_\Omega{L_{light}dw_i}\ =&\frac{albedo}{\pi}I_q\ =&\frac{albedo}{\pi}\frac{\Phi_q}{dA} \end{align} $$

此外，由于着色位置p点和间接光源q点之间visibility难以计算，通常认为其总是1，即所有次级光源发射的间接光都可以被其他点接收到。由此，进一步化简p点处出射间接光。

$$ \begin{align} E_o(p,w_o)=\frac{albedo}{\pi}\Phi_q\frac{cos\theta_{p}cos\theta_{q}}{||p-q||^2} \end{align} $$

Problem：

• 次级光源到着色点的可见性没法计算；
• 次级光源总是被视为diffuse的。

Acceleration：

按照RSM算法的逻辑，需要将阴影贴图中所有点都视作次级光源，显然计算量太大。一个不错的加速办法就是引入权重，即尽量多考虑距离着色点近的次级光源，这样就避免了大量计算。

Light Propagation Volumes

光照传播体积（Light Propagation Volumes, LPV）同样是一种3D空间的全局光照算法。

Steps：

• 通过阴影贴图找出所有直接光源照亮的片元，并将它们作为次级光源；
• 将这些次级光源放入划分好的3d网格中；
• 计算所有次级光源传播到它周围六个格子中的辐射度（类似RSM，仍然不考虑visibility的问题），迭代直到辐射度稳定；
• 根据这些辐射度进行渲染。

Voxel Global Illumination

Screen Space Ambient Occlusion

环境光遮蔽（Ambient Occlusion, AO）是一种简单全局光照技术。它通过计算物体之间相互遮挡而导致的间接光衰减，进而刻画出相邻物体间隙的明暗。

具体来说，AO技术基于一个假设，即任何一个着色点的间接光都是常数，且只考虑diffuse。由此，该位置的渲染方程由此可以化简为：

$$ L_o^{indir}(x, w_o)=\int_H^2L_i^{indir}(x, w_i)f_r(x, w_o, w_i)V(x, wi)cos\theta dw_i\ L_o^{indir}(x, w_o)=L_i^{indir}f_r\int_H^2V(x, wi)cos\theta dw_i\ $$

Ambient Map：

早期的AO技术以预计算为主。它使用光线追踪得到一张AO贴图，即原理中提到的关于visibility的积分，从而在实时渲染中实现环境光遮蔽效果。不过这种方法的缺点也比较明显，它需要额外的纹理存储，且只能表现静态场景。

SSAO Algorithm：

屏幕空间环境光遮蔽(Screen Space Ambient Occlusion, SSAO)是对预计算AO贴图的一种改进。它只利用屏幕空间的信息就可以实时的计算出上述提到的visibility积分。其核心是根据实时计算中得到的z-buffer信息得出着色点之间的相互遮挡情况。

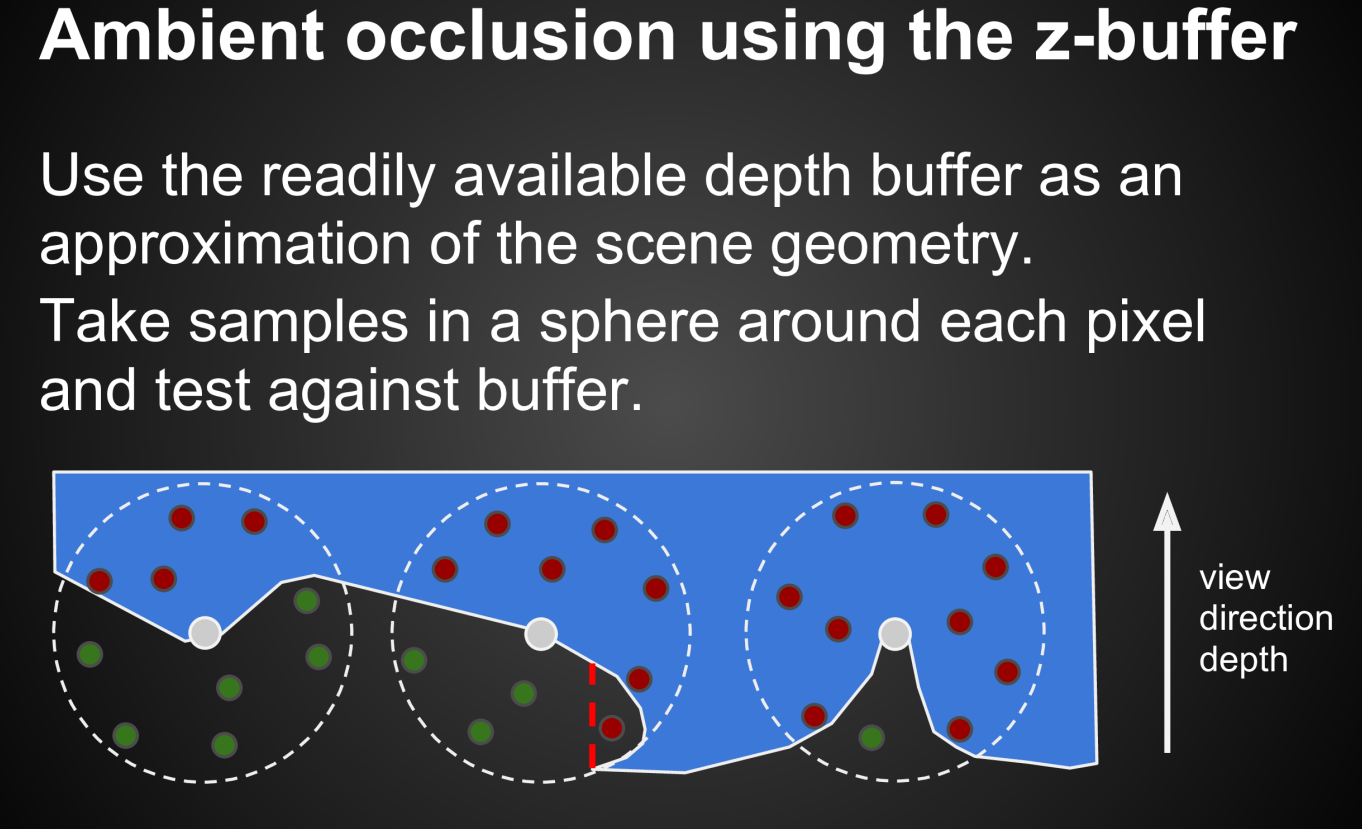
具体来说，它使用蒙塔卡洛来计算上述积分，即：

• 在当前着色点周围采样一定数量的点；
• 计算出采样点的深度，将其和阴影贴图中相应位置的深度比较，得出是否能接受到直接光。换句话说，只要采样点能接收到直接光，就认为它发出的间接光一定会被着色点接收到。

SSAO Problem：

• 只采样有限范围的点，即较远位置发出的间接光对着色点没有考虑；
• 理论上应该计算的是着色点到采样点的visibility，但在实践中只考虑的采样点到光源的visibility。
• 采样球，能量会不守恒。
• 由于没有法线信息，无法考虑cos。

Horizon Based Ambient Occlusion+

屏幕空间水平基准环境光遮蔽（Horizon Based Ambient Occlusion, HBAO）是对SSAO的一种改进。它整体和SSAO思路类似。只不过HBAO要求获取着色点法线信息，因此它可以采样半球同时考虑cos。此外，HBAO还引入的了光线步进(Ray Marching)来计算采样点到着色点之间的可见性，从而大大增强了其真实性。

Screen Space Directional Occlusin

屏幕空间的方向性遮挡（Screen Space Directional Occlusin, SSDO）也是一种屏幕空间的全局光照技术。它的做法整体和SSAO或HBAO类似，也即在半球中采样一系列点，判断这些点是否为次级光源，从而计算该着色点处间接光。

SSAO vs SSDO：

不过，SSAO和SSDO判断采样点是否为次级光源不同。SSDO认为采样点被折叠时为次级光源，而SSAO则相反。这也是这两者方法的核心区别，即对间接光来源的假设不同。

如下图所示，SSAO假设间接光来自较远的位置（红色圈部分）；而SSDO则假设间接光来自较近位置的弹射（橙色圈）。

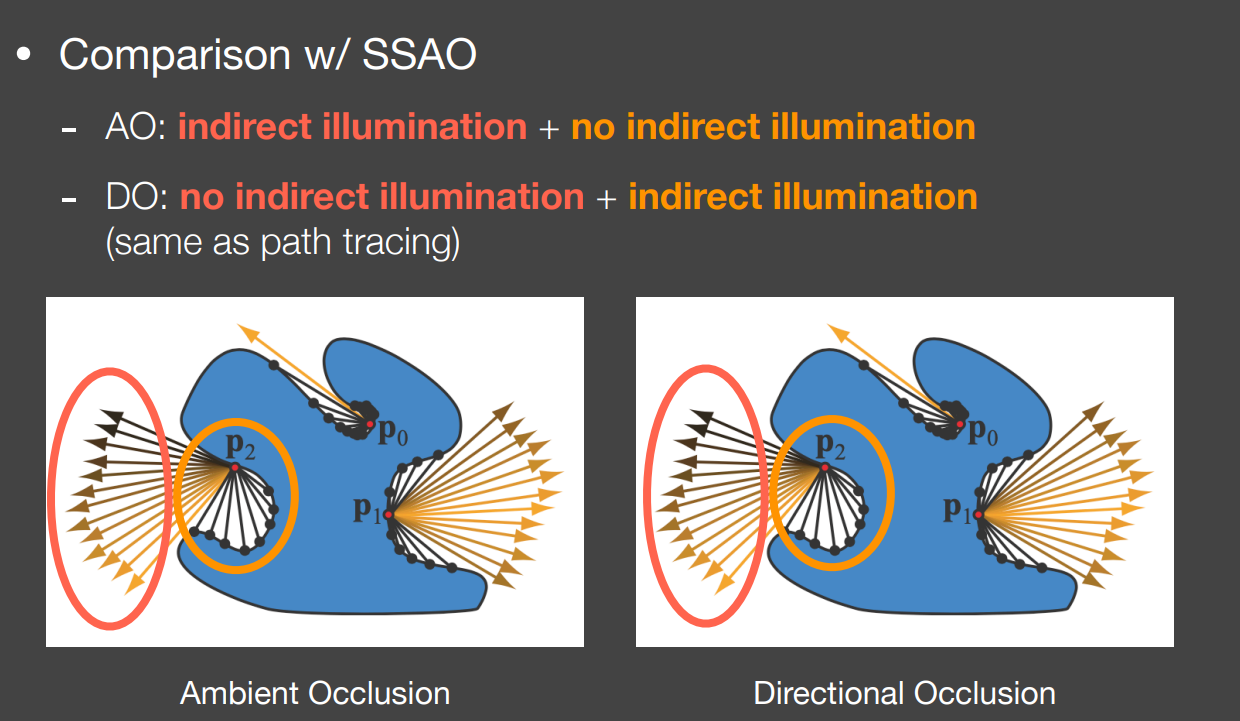
Problem：

类似SSAO，SSDO也假设采样点如果是次级光源，那么着色点一定会接收到间接光。即，使用光源视角下采样点的可见性代替了着色点视角下采样点的可见性。

这样就会造成如上图第三个例子中的问题。在SSDO算法中，P到A没有被挡住，那么A对P不会产生间接光。然而，在实际实现中，A在shadow map被挡住，我们反而认为A点会产生间接光，这显然不合理。

除此之外，SSDO另外的问题则是其只能感受小范围的间接光，因为采样范围有限。

Screen Space Reflection

屏幕空间反射（Screen Space Reflection, SSR）是一种屏幕空间的全局光照技术。具体来说，它利用屏幕空间信息进行光线追踪。因此，和AO技术相比，SSR不仅仅考虑diffuse的间接光，同样也可以计算specular的间接光。

Ray Marching：

光线步进（Ray Marching）是SSR中进行光线追踪的方法。根据实现不同，又可分为线性光线步进（Linear Ray Marching）和层次光线步进（Hierarchical Ray Marching）。其中，线性光线步进每次沿着追踪方向前进固定步长，其使用GLSL实现的代码如下：

bool RayMarch(vec3 ori, vec3 dir, out vec3 hitPos) {
  hitPos = ori;
  for (int i = 0; i < 100; i++) {
    hitPos += dir * STEP_LEN;
    float depth = GetDepth(hitPos);
    float gDepth = GetGBufferDepth(GetScreenCoordinate(hitPos));
    if (gDepth > depth) {
      return true;
    }
  }
  return false;
}

至于层次光线步进，它每次前进的步长则是自适应的，有点类似网络中拥塞窗口的变化。其执行流程如下：

• 首先，将发生反射/光线追踪的视锥切分成固定大小的格子；
• 接着，开始光线步进；
  • 若没发生碰撞，则将步长翻倍，继续前进；
  • 反之，缩短步长为二分之一，直到步长为1时，跳出循环。
• 返回碰撞点。